Insight Maker includes built-in optimization functionality to automatically adjust one or more variable values in order to achieve a desired goal.

Imagine a model of a company that would forecast future revenue for the company. Of the variables managers have control over, let's assume that there are two they are particularly curious about: how much to invest in marketing and how much to invest in research and development. Using the company's model, the managers could experiment with different values for these parameters and see how they affected revenues. They could even seek to find the combination of values that maximized revenue. However, it might take a very long time and a lot of experimentation in order to find the precise combination of values that did this. Using the optimizer function of Insight Maker, you can have Insight Maker very quickly search through a wide range of values to find the set that best achieves a certain goal such as maximizing revenue.

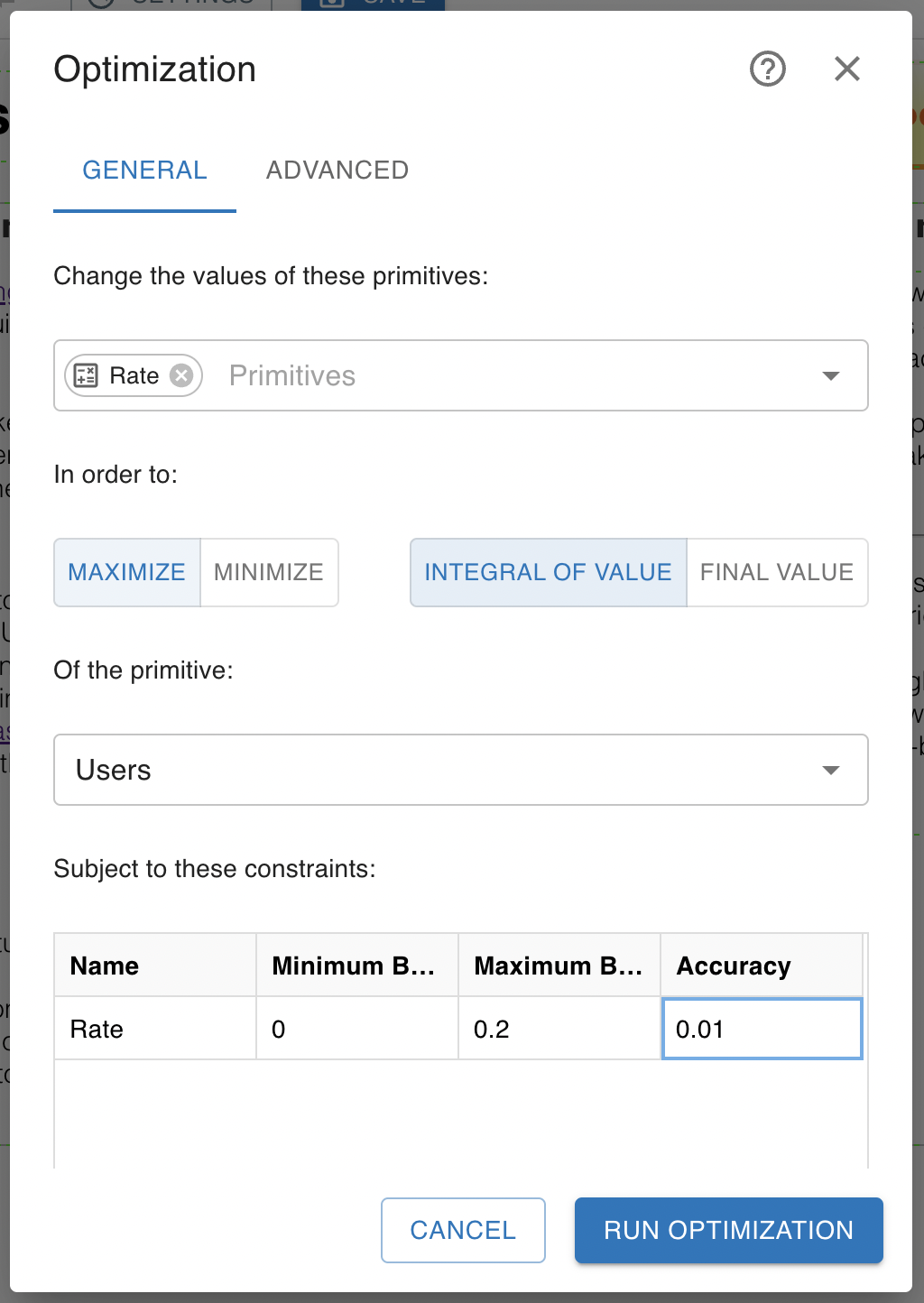
There are several key options that must be configured when setting up the optimizer. These include:

• Goal Primitive: This is the primitive that you want to influence. In the business example, it is the revenue taken in by the company.
• Goal: This is what we want to do to the goal primitive. It is either to maximize the primitive (which would be the desired case for revenue) or to minimize it if the goal primitive represented a measure of cost or error.
• Goal Type: If we only care about the final value of the revenue, we would use the "Final Value" goal type. If, however, we wanted to maximize the revenue over all years in the simulation, we would use the "Integral" goal type.
• Primitives to Change: These are the primitives Insight Maker automatically changes to achieve the goal. In the model of the company we want to adjust the marketing expenses along with the research and development expenses.
• Bounds: For the primitives that will be adjusted, you need to specify an upper and lower bound. Insight Maker will adjust the primitive values within these bounds.
• Accuracy: This is the minimum desired level of accuracy for that primitive value. Once Insight Maker has moved the primitive value to within that range of where it knows the true value should be, it will stop optimizing and show you the results. The smaller the accuracy, the longer the optimization will take.

Once these options are configured, you can press the Optimize button and Insight Maker will automatically search to find the best values for the parameters. This optimization may take some time. The length of optimization time increases exponentially with the number of primitives to change, so it is best to start with just one or two and increase your scope slowly from there. In addition to these configuration options, there are also a set of advanced options:

• Random Starts: The optimizer uses a deterministic optimization algorithm. When you have local minimums or maximums in the solution space, it might locate one of those instead of the global maximum or minimum. You can use random starting locations to carry out a more comprehensive search of the parameter space and gain confidence you have found the true global optimum.
• Maximum Number of Iterations: The optimizer will stop when all the parameter values are within their desired accuracy of the true values. If this is taking too long and you want it to stop earlier, you can specify a maximum number of iterations prior to stopping.
• Step Reduction Factor: This controls how fast the optimizer narrows in on a value.

One typical use of the optimizer is to fit a model to historical data. Imagine we had historical revenue data in addition to the simulated revenue values in the business model. Rather than trying to maximize revenue, we would like to adjust the parameter values in the model in order to make the simulated data best match the historical data. We can do this using the optimizer by first creating a variable in the model that measures the error for the fit of the simulated to historical data. We could use, for example, classic squared error:

([Simulated Revenue] - [Historical Revenue])^2

Or we could use a more robust measure of error that is less sensitive to outliers:

Abs([Simulated Revenue] - [Historical Revenue])

Then we could use the "Integral" goal type to minimize the value of this variable in order to optimize our model's fit to the historical data.